
fig 4.1
Integers are coded in 2-complement and overflows are silently ignored
by Pike. This means that if your integers are 32-bit and you add 1 to
the number 2147483647 you get the number -2147483648. This works exactly
as in C or C++.
All the arithmetic, bitwise and comparison operators can be used on integers.
Also note these functions:
All the arithmetic and comparison operators can be used on floats.
Also, these functions operates on floats:
You might be surprised to see that individual characters can have values
up to 2³²-1 and wonder how much memory that use. Do not worry, Pike
automatically decides the proper amount of memory for a string, so all
strings with character values in the range 0-255 will be stored with
one byte per character. You should also beware that not all functions
can handle strings which are not stored as one byte per character, so
there are some limits to when this feature can be used.
Although strings are a form of arrays, they are immutable. This means that
there is no way to change an individual character within a string without
creating a new string. This may seem strange, but keep in mind that strings
are shared, so if you would change a character in the string "foo",
you would change *all* "foo" everywhere in the program.
However, the Pike compiler will allow you to to write code like you could
change characters within strings, the following code is valid and works:
4.1 Basic types
The basic types are int, float and string.
For you who are accustomed to C or C++, it may seem odd that a string
is a basic type as opposed to an array of char, but it is surprisingly
easy to get used to.
4.1.1 int
Int is short for integer, or integer number. They are normally
32 bit integers, which means that they are in the range -2147483648 to
2147483647. Note that on some machines an int might be larger
than 32 bits. Since they are integers, no decimals are allowed. An integer
constant can be written in several ways:
All of the above represent the number 78. Octal notation means that
each digit is worth 8 times as much as the one after. Hexadecimal notation
means that each digit is worth 16 times as much as the one after.
Hexadecimal notation uses the letters a, b, c, d, e and f to represent the
numbers 10, 11, 12, 13, 14 and 15. The ASCII notation gives the ASCII
value of the character between the single quotes. In this case the character
is N which just happens to be 78 in ASCII.
78 // decimal number
0116 // octal number
0x4e // hexadecimal number
'N' // Ascii character4.1.2 float
Although most programs only use integers, they are unpractical when doing
trigonometric calculations, transformations or anything else where you
need decimals. For this purpose you use float. Floats are normally
32 bit floating point numbers, which means that they can represent very large
and very small numbers, but only with 9 accurate digits. To write a floating
point constant, you just put in the decimals or write it in the exponential
form:
Of course you do not need this many decimals, but it doesn't hurt either.
Usually digits after the ninth digit are ignored, but on some architectures
float might have higher accuracy than that. In the exponential form,
e means "times 10 to the power of", so 1.0e9 is equal to
"1.0 times 10 to the power of 9".
3.14159265358979323846264338327950288419716939937510 // Pi
1.0e9 // A billion
1.0e-9 // A billionth4.1.3 string
A string can be seen as an array of values from 0 to 2³²-1.
Usually a string contains text such as a word, a sentence, a page or
even a whole book. But it can also contain parts of a binary file,
compressed data or other binary data. Strings in Pike are shared,
which means that identical strings share the same memory space. This
reduces memory usage very much for most applications and also speeds
up string comparisons. We have already seen how to write a constant
string:
As you can see, any sequence of characters within double quotes is a string.
The backslash character is used to escape characters that are not allowed or
impossible to type. As you can see, \t is the sequence to produce
a tab character, \\ is used when you want one backslash and
\" is used when you want a double quote (") to be a part
of the string instead of ending it.
Also, \XXX where XXX is an
octal number from 0 to 37777777777 or \xXX where XX
is 0 to ffffffff lets you write any character you want in the
string, even null characters. From version 0.6.105, you may also use
\dXXX where XXX is 0 to 2³²-1. If you write two constant
strings after each other, they will be concatenated into one string.
"hello world" // hello world
"he" "llo" // hello
"\116" // N (116 is the octal ASCII value for N)
"\t" // A tab character
"\n" // A newline character
"\r" // A carriage return character
"\b" // A backspace character
"\0" // A null character
"\"" // A double quote character
"\\" // A singe backslash
"\x4e" // N (4e is the hexadecimal ASCII value for N)
"\d78" // N (78 is the decimal ACII value for N)
"hello world\116\t\n\r\b\0\"\\" // All of the above
"\xff" // the character 255
"\xffff" // the character 65536
"\xffffff" // the character 16777215
"\116""3" // 'N' followed by a '3'
However, you should be aware that this does in fact create a new string and
it may need to copy the string s to do so. This means that the above
operation can be quite slow for large strings. You have been warned.
Most of the time, you can use replace, sscanf, `/
or some other high-level string operation to avoid having to use the above
construction too much.
string s="hello torld";
s[6]='w';
All the comparison operators plus the operators listed here can be used on strings:
Also, these functions operates on strings:
As you can see, each element in the array can contain any type of value. Indexing and ranges on arrays works just like on strings, except with arrays you can change values inside the array with the index operator. However, there is no way to change the size of the array, so if you want to append values to the end you still have to add it to another array which creates a new array. Figure 4.1 shows how the schematics of an array. As you can see, it is a very simple memory structure.({ }) // Empty array
({ 1 }) // Array containing one element of type int
({ "" }) // Array containing a string
({ "", 1, 3.0 }) // Array of three elements, each of different type

Operators and functions usable with arrays:
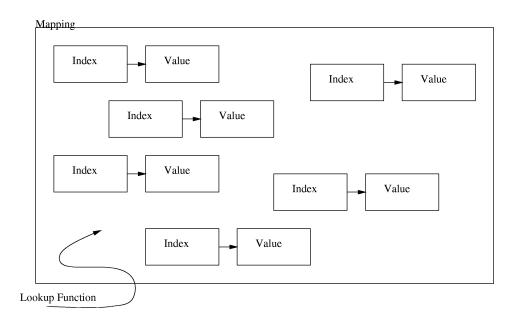
Each index-value pair is floating around freely inside the mapping. There is exactly one value for each index. We also have a (magical) lookup function. This lookup function can find any index in the mapping very quickly. Now, if the mapping is called m and we index it like this: m [ i ] the lookup function will quickly find the index i in the mapping and return the corresponding value. If the index is not found, zero is returned instead. If we on the other hand assign an index in the mapping the value will instead be overwritten with the new value. If the index is not found when assigning, a new index-value pair will be added to the mapping. Writing a constant mapping is easy:
([ ]) // Empty mapping
([ 1:2 ]) // Mapping with one index-value pair, the 1 is the index
([ "one":1, "two":2 ]) // Mapping which maps words to numbers
([ 1:({2.0}), "":([]), ]) // Mapping with lots of different types
As with arrays, mappings can contain any type. The main difference is that the index can be any type too. Also note that the index-value pairs in a mapping are not stored in a specific order. You can not refer to the fourteenth key-index pair, since there is no way of telling which one is the fourteenth. Because of this, you cannot use the range operator on mappings.
The following operators and functions are important:
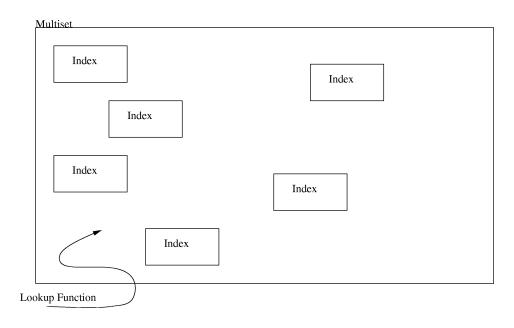
Instead, the index operator will return 1 if the value was found in the multiset and 0 if it was not. When assigning an index to a multiset like this: mset[ ind ] = val the index ind will be added to the multiset mset if val is true. Otherwise ind will be removed from the multiset instead.
Writing a constant multiset is similar to writing an array:
Note that you can actually have more than one of the same index in a multiset. This is normally not used, but can be practical at times.(< >) // Empty multiset
(< 17 >) // Multiset with one index: 17
(< "", 1, 3.0, 1 >) // Multiset with 3 indices
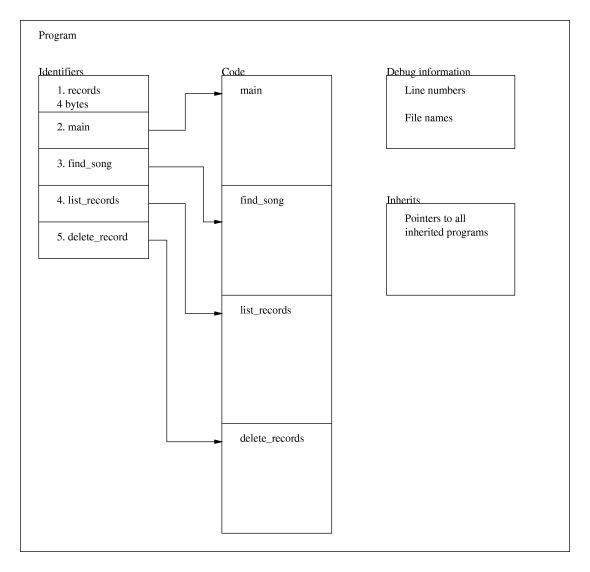
You can also use the cast operator like this:program p = compile_file("hello_world.pike");
This will also load the program hello_world.pike, the only difference is that it will cache the result so that next time you do (program)"hello_world" you will receive the _same_ program. If you call compile_file("hello_world.pike") repeatedly you will get a new program each time.program p = (program) "hello_world";
There is also a way to write programs inside programs with the help of the class keyword:
The class keyword can be written as a separate entity outside of all functions, but it is also an expression which returns the program written between the brackets. The class_name is optional. If used you can later refer to that program by the name class_name. This is very similar to how classes are written in C++ and can be used in much the same way. It can also be used to create structs (or records if you program Pascal). Let's look at an example:class class_name {
inherits, variables and functions
}
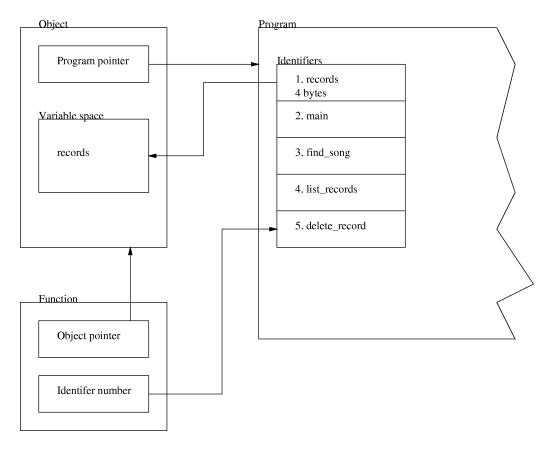
This could be a small part of a better record register program. It is not a complete executable program in itself. In this example we create a program called record which has three identifiers. In add_empty_record a new object is created by calling record. This is called cloning and it allocates space to store the variables defined in the class record. Show_record takes one of the records created in add_empty_record and shows the contents of it. As you can see, the arrow operator is used to access the data allocated in add_empty_record. If you do not understand this section I suggest you go on and read the next section about objects and then come back and read this section again.class record {
string title;
string artist;
array(string) songs;
}
array(record) records = ({});
void add_empty_record()
{
records+=({ record() });
}
void show_record(record rec)
{
write("Record name: "+rec->title+"\n");
write("Artist: "+rec->artist+"\n");
write("Songs:\n");
foreach(rec->songs, string song)
write(" "+song+"\n");
}
compile_file simply reads the file given as argument, compiles it and returns the resulting program. compile_string instead compiles whatever is in the string p. The second argument, filename, is only used in debug printouts when an error occurs in the newly made program. Both compile_file and compile_string calls compile to actually compile the string after calling cpp on it.program compile(string p);
program compile_file(string filename);
program compile_string(string p, string filename);
The following operators and functions are important:
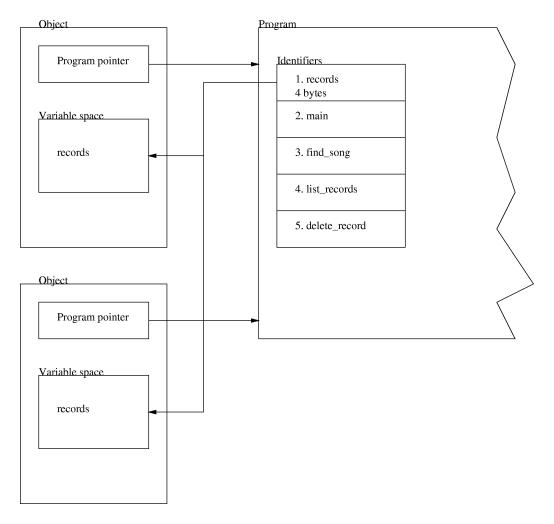
Here we can clearly see how the function show prints the contents of the variables in that object. In essence, instead of accessing the data in the object with the -> operator, we call a function in the object and have it write the information itself. This type of programming is very flexible, since we can later change how record stores its data, but we do not have to change anything outside of the record program.class record {
string title;
string artist;
array(string) songs;
void show()
{
write("Record name: "+title+"\n");
write("Artist: "+artist+"\n");
write("Songs:\n");
foreach(songs, string song)
write(" "+song+"\n");
}
}
array(record) records = ({});
void add_empty_record()
{
records+=({ record() });
}
void show_record(object rec)
{
rec->show();
}
Functions and operators relevant to objects:
In this example, the function bar returns a pointer to the function foo. No indexing is necessary since the function foo is located in the same object. The function gazonk simply calls foo. However, note that the word foo in that function is an expression returning a function pointer that is then called. To further illustrate this, foo has been replaced by bar() in the function teleledningsanka.int foo() { return 1; }
function bar() { return foo; }
int gazonk() { return foo(); }
int teleledningsanka() { return bar()(); }
For convenience, there is also a simple way to write a function inside another function. To do this you use the lambda keyword. The syntax is the same as for a normal function, except you write lambda instead of the function name:
The major difference is that this is an expression that can be used inside an other function. Example:lambda ( types ) { statements }
This is the same as the first two lines in the previous example, the keyword lambda allows you to write the function inside bar.function bar() { return lambda() { return 1; }; )
Note that unlike C++ and Java you can not use function overloading in Pike. This means that you cannot have one function called 'foo' which takes an integer argument and another function 'foo' which takes a float argument.
This is what you can do with a function pointer.
This program will of course write Hello world.int main(int argc, array(string) argv)
{
array(string) tmp;
tmp=argv;
argv[0]="Hello world.\n";
write(tmp[0]);
}
Sometimes you want to create a copy of a mapping, array or object. To do so you simply call copy_value with whatever you want to copy as argument. Copy_value is recursive, which means that if you have an array containing arrays, copies will be made of all those arrays.
If you don't want to copy recursively, or you know you don't have to copy recursively, you can use the plus operator instead. For instance, to create a copy of an array you simply add an empty array to it, like this: copy_of_arr = arr + ({}); If you need to copy a mapping you use an empty mapping, and for a multiset you use an empty multiset.
As you can see there are some interesting ways to specify types. Here is a list of what is possible:int x; // x is an integer
int|string x; // x is a string or an integer
array(string) x; // x is an array of strings
array x; // x is an array of mixed
mixed x; // x can be any type
string *x; // x is an array of strings
// x is a mapping from int to string
mapping(string:int) x;
// x implements Stdio.File
Stdio.File x;
// x implements Stdio.File
object(Stdio.File) x;
// x is a function that takes two integer
// arguments and returns a string
function(int,int:string) x;
// x is a function taking any amount of
// integer arguments and returns nothing.
function(int...:void) x;
// x is ... complicated
mapping(string:function(string|int...:mapping(string:array(string)))) x;